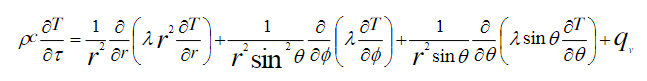扫描文末二维码,关注这个学化工的厨子。
每周六下午六点,公众号内定时发布
欢迎将文章分享到朋友圈
文/神探玺洛克
一眨眼过完年已经十几天了,下周就是“元宵节”!!!
古人称”夜”为“宵”,而正月又是农历的元月,所以人们把正月十五这第一个月圆之夜称为元宵节。据传,西汉时人们就开始过元宵节,汉武帝正月上辛夜在甘泉宫祭祀“太一”的活动。在汉魏之后,正月十五元宵节渐渐成为一个民俗节日。
正月十五这天北方吃元宵,南方吃汤圆。以前玺洛克只知道两个都是圆的,夏三哥告诉玺洛克“元宵”的馅是硬的,切成块沾水后放在糯米粉里摇成团;而“汤圆”则是用剂子加馅包出来的。
后来玺洛克从超市里买了两包对比了一下。从口感上讲,元宵是硬馅加表面干粉,混汤吃很有嚼劲;汤圆则吃起来软滑细腻,丝毫没有大颗粒的感觉。
元宵和汤圆都用糯米制成,大家都知道糯米是黏的,但糯米为什么是黏的呢?
从物质的组成结构上讲,糯米等多糖由葡萄糖等单糖组成。普通大米含有许多直链淀粉和支链淀粉,直链淀粉分子的所有部分都可以和水分子密切接触,且分子中含有大量亲水的羟基,所以直链淀粉能溶于热水,较难形成胶体溶液,黏性不强;而糯米只含支链淀粉,水分子难以进入多糖分子内部,在热水中分子只是“膨大”,并不能完全溶于水,从而形成胶体溶液,所以黏性较强。
好了,下面进入正题:一个学化工的厨子来教你怎么煮汤圆!!!
我们从化工传热的角度进行分析:
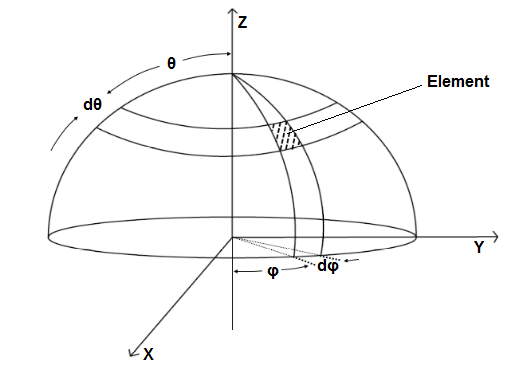
因为汤圆是圆形的,所以我们可以对汤圆建立一个球坐标系:
在这个球坐标系里,我们对汤圆的传热过程建立热传递方程,具体过程式子比较多,我们就先省略,只给大家把推导后方程列出来:
因为汤圆包括糯米皮和芝麻馅两部分,所以我们分成糯米皮(厚度约0.3 cm)部分和芝麻馅(厚度约1.5 cm)两部分分别进行处理。
方程中的$\rho$为糯米皮或芝麻馅的密度。糯米的密度一般在410-490 kg/m3左右,我们此处取450 kg/m3。因为糯米皮是糯米面和水按照500:300 (wt%)的比例混合的,所以我们按照混合规则处理糯米和水的性质参数得到糯米面的性质参数。芝麻馅是炒制而成的,所以其密度参照白芝麻(565.49-630.49 kg/m3),与含水量的关系为:
$\rho_{ws}=-4.0997M+647.01 (R^2=0.999)$
c为比热容,参照文献,对于糯米(1.27-4.83 kJ/kg•K)我们取为温度的函数。因为水温超过53 ℃时淀粉会逐渐发生糊化,所以我们选定超过淀粉糊化温度段的函数:
$c_g=-0.025+7.0205 (R^2=0.997)$
对于芝麻馅(1.062-3.058 kJ/kg•K)则有:
$c_{ws}=-214.454+292.079M+16.248T-8.015 M^2+0.289T^2-4.257MT+0.145TM^2 (R^2=0.98)$
$\lambda$为糯米的导热系数(0•086-0•158 W/m℃),参照文献我们取为水含量、温度和密度的函数:
$\lambda_g=-0.0943+3.87\times 10^{-3} M+6.19\times 10^{-4} T+3.14\times 10^{-4} \rho_g$
对于芝麻馅(0•031-0•149 W/m/℃):
$\lambda_{ws}=-0.008+0.003M+0.001T+5.058\times 10^{-6} MT (R^2=0.95)$
为了求解这个方程,我们还需要一些条件:初值条件和边界条件。初始状态下,汤圆刚从冰箱里面取出,玺洛克实验室冰箱的冷藏室是-20 ℃,所以我们就假设初始状态为汤圆内各处温度均为-20 ℃。 接下来是边界条件,汤圆中心温度对称,所以中心温度T对位置r的偏导为0;糯米皮与芝麻馅处热通量相等,所以界面两边温度对位置r的偏导相等;汤圆外缘始终处于沸水中,所以我们假定汤圆与水接触的表面温度T恒为100 ℃。
有了这些热量传递方程和限制条件之后,玺洛克用Matlab对其进行求解,得到了半径1.8 cm的汤圆的径向温度分布随时间变化图像:
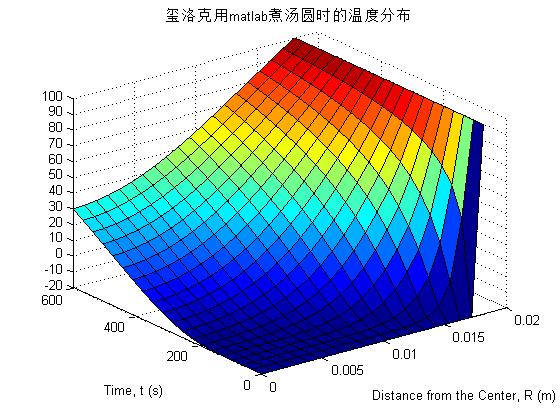
由图可知,最初汤圆各处都处于-20 ℃,随着煮制时间的增加,汤圆的温度由外向内逐渐增加。若水温恒为100 ℃,则汤圆煮10分钟左右就可以吃了。
但是水温一直保持在100 ℃的话就会存在一个问题:
沸水滚大浪,皮馅一锅汤。
所以,煮汤圆和元宵要“滚水下、慢火煮”,水沸时加适量凉水,保持似滚非滚的状态。最好用汤勺轻轻推转汤圆,避免汤圆粘锅。
不过,在煮元宵时玺洛克还注意到一个问题,为啥汤圆一直在打滚呀?
从传热的角度讲,水的热对流肯定是其中的原因之一。锅中热水温度分布不均匀,其热对流带来的扰动使得元宵发生旋转,从而使得汤圆表面受热更加均匀。
此外,汤圆在水中分为水下和水上两部分,其水上部分暴露于空气中,受冷收缩,体积减小,密度增大,使得整个汤圆的重心上移。
伴随着热水对流的扰动,汤圆重心偏离原来球形的中心线而旋转,直到重心重新回到汤圆的中心线,此时汤圆发生180°翻转。
好了,玺洛克来实践一下,以中*牌花生白芝麻汤圆为例:

从冰箱里拿出来放到烧开的沸水里面:

放进汤圆后水汤圆附近水温下降,水停止沸腾,然后我们就可以盖上盖子等了(7:32 am 17/02/2019)。
8分钟后,水开始沸腾,此时加一点凉白开,然后稍微用勺子背推转一下元宵(7:40 am 17/02/2019)。

过了3min,水再次沸腾,捞一个用筷子插一下:
嗯,已经煮熟了,上桌!

但问题来了,汤圆煮多了吃不完怎么办?
给玺洛克吃呀~再吃不完的汤圆可以冷冻起来,不过汤圆的冷冻也是有讲究的。不同冷冻温度和冷冻时间对汤圆的品质有显著性影响。
随着冷冻时间的延长,汤圆含水率先下降后平缓,馅料油脂氧化则先急后缓的上涨,硬度和咀嚼性也随着冷冻时间的延长而逐渐增加。此外,冷冻温度越高,水分子自由度越大,汤圆含水率下降越多,同时馅料油脂氧化程度越高、硬度、咀嚼性增加越大。所以,自由水与半结合水的迁移变化是引起汤圆变质的根本原因,而-25 ℃左右的冷冻可以有效的抑制速冻汤圆变质。
所以,吃不完的一定要放在冷冻里!!
但话说回来,糯米性温,黏性大,不易消化且碳水化合物、脂肪、糖含量较高,《随息居饮食谱》记载:“糯米,性太黏滞,难化也。小儿、病人最宜忌之。”
汤圆虽好,可不要贪吃噢。
参考资料:
- 李菁,《香甜汤圆莫贪多》,健康报,2018
- 刘桂云,《汤圆的几种吃法》,科学与生活,2018
- 张怀华,《汤圆自动翻身现象探秘》,物理教学,2017
- 潘治利等,《不同冻藏温度条件下速冻汤圆品质变化及其机制》,农业工程学报,2018
- 周显青等,《加工条件对汤圆蒸煮特性的影响及水分迁移分析》,粮油食品科技,2015
- So What Exactly Is Sticky Rice, Anyway?(https://www.huffpost.com/entry/sticky-rice_n_6084408)
- V.V.Sreenarayanan,《Thermal conductivity and diffusivity of rice bran》,Journal of Agricultural Engineering Research,1986
- Determination_of_Specific_Heat_and_Gelatinization_Temperature_of_Rice_using_Differential_Scanning_Calorimetry (https://www.researchgate.net/publication/271432160_Determination_of_Specific_Heat_and_Gelatinization_Temperature_of_Rice_using_Differential_Scanning_Calorimetry)
- Debabandya Mohapatra,《Determination of Specific Heat and Gelatinization Temperature of Rice using Differential Scanning Calorimetry 》,The Society for Engineering, Agricultural, Food, and Biiological System
- 淀粉糊化-百度百科(https://baike.baidu.com/item/%E6%B7%80%E7%B2%89%E7%B3%8A%E5%8C%96)
- Mashhad, Iranm,《EFFECT OF MOISTURE CONTENT AND TEMPERATURE ON THERMAL BEHAVIOUR OF SESAME SEED》, The Annals of the University Dunarea de Jos of Galati Fascicle VI – Food Technology, 2014
扫描文末二维码,欢迎关注微信在公众号“神探玺洛克”,每周六下午六点更新,吃着核桃来读书。
function pdex1
clear
clear all
%Note:
%1.本例中白芝麻比热容和导热系数算出的结果稍大与理论范围,一方面可能是因为温度超出公式适用范围导致的;也可能是因为本例固定了水含量而水含量实际是变化的。
%----------------------------------
%汤圆半径r_t=0.014m,糯米皮厚d_n=0.002m,芝麻馅半径r_z = r_t - d_n
global r_z
r_t = 0.013;
d_n = 0.003;
r_z = r_t - d_n;
x = linspace(0,r_t,20);
t = linspace(0,600,20);
m = 2;
sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
%-------------------
%画图
u = sol(:,:,1);
surf(x,t,u)
title('玺洛克用matlab煮汤圆时的温度分布')
xlabel('Distance from the Center, R (m)')
ylabel('Time, t (s)')
set(gca,'ztick',[-20:10:100])
%=======================================================================
%
function [c,f,s] = pdex1pde(x,t,u,DuDx)
global r_z
T = u;
%糯米的性质参数
M_m = 0.1*100;%含水量
%糯米密度~410-490 kg/m3
rho_m = 450;
%糯米导热系数~0?086-0?158 W/m/K
k_m = -0.0943+3.87e-3.*M_m+6.19e-4.*T+3.14e-4.*rho_m;
%糯米比热容 1.27e3-4.83e3 J/kg/K
c_m = (-0.025.*u+7.0205)*1e3;
%水的性质参数
rho_w = 997;
k_w = (0.683-0.599)./(100-20).*(T-20);%插值水的导热系数W/m/K
c_w = 4.2*1e3;%比热容J/kg/K
%糯米面团的性质参数
%糯米面与水的质量比为500:300 (wt%,g)
rho_n = rho_m.*5/8+rho_w.*3/8;
k_n = k_m.*5/8+k_w.*3/8;
c_n = c_m.*5/8+c_w.*3/8;
%---------------
%芝麻的性质参数
%---------------
M_z = 0.2*100;
%芝麻密度 565.49-630.49 kg/m3
rho_z = -4.0997*M_z+647.01;
%芝麻导热系数 0?031-0?149 W/m°C
k_z = -0.008+0.003*M_z+0.001*T+5.058e-6*M_z*T;
%芝麻比热容 1.062-3.058 kJ/kg?K
c_z = -214.454+292.079*M_z+16.248*T-8.015*M_z^2+0.289*T^2-4.257*M_z*T+0.145*T*M_z^2;
%微分方程参数
f = DuDx;
s = 0;
%针对芝麻馅和糯米皮进行参数的分段处理
if x >= r_z
c = rho_n*c_n/k_n;
else
c = rho_z*c_z/k_z;
end
%=======================================================================
%边界条件
function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
%if mod(t,60) == 0
tw = 100;
%else
% tw = 90
%end
%tc = -20;
pl = 0;
ql = 1;%中心温度对称
pr = ur-tw;%外部温度为tw
qr = 0;
%=======================================================================
%初始条件
function u0 = pdex1ic(x)
u0 = -20;%初始温度
手机版“神探玺洛克”请扫码